참고 영상
나동빈 유튜브 이코테 2021 강의 몰아보기 : DFS & BFS
많은 양의 데이터 중에서 원하는 데이터를 찾는 과정을 탐색이라고 한다.
DFS & BFS는 대표적인 그래프 탐색 알고리즘이다.
DFS 와 BFS를 공부하기전에 무조건 알아야 할 자료구조 두 가지
스택과 큐를 알아야 한다.
스택
먼저 들어 온 데이터가 나중에 나가는 형식(선입후출)의 자료구조
대표적인 예시 : 박스 쌓기
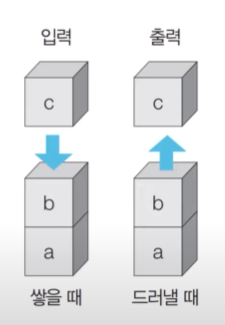
스택 자료구조는 삽입과 삭제의 연산으로 이루어진다.
파이썬에서 스택을 사용하려면 단순하게 list로 사용하면 된다.
stack = []
stack.append(1) # 1
stack.append(3) # 1 - 3
stack.append(5) # 1 - 3 - 5
stack.append(7) # 1 - 3 - 5 - 7
stack.pop() # 1 - 3 - 5
stack.append(9) # 1 - 3 - 5 - 9
stack.pop() # 1 - 3 - 5
print(stack) # print : [1, 3, 5]
큐
먼저 들어 온 데이터가 먼저 나가는 형식(선입선출)의 자료구조이다.
대표적인 예시 : 터널
from collections import deque
queue = deque()
queue.append(1) # 1
queue.append(2) # 1 - 2
queue.append(3) # 1 - 2 - 3
queue.append(4) # 1 - 2 - 3- 4
queue.popleft() # 2 - 3 - 4
queue.append(5) # 2 - 3 - 4 - 5
queue.popleft() # 3 - 4 - 5
print(queue) # print : deque([3, 4, 5])
queue.reverse()
print(queue) # print : deque([5, 4, 3])collections 라이브러리에서 deque를 가져와서 사용한다.
재귀 함수(Recursive Function)
자기 자신을 다시 호출하는 함수
DFS를 실제로 구현하고자 할 때 꼭 사용하는 내용이기 때문에 알아야 한다.
def recursive():
print("함수 호출")
recursive()
recursive()
# 출력
# "함수 호출"
# "함수 호출"
# "함수 호출"
# "함수 호출"
# "함수 호출"
# "함수 호출"
# "함수 호출"
# "함수 호출"
# "함수 호출"
# ...
재귀 함수에서는 재귀 함수의 종료 조건을 "반드시" 명시해야 한다.
종료 조건이 없다면 빠져나갈 부분이 없어서 무한 반복 될 수 있다.
i = 0
def recursive(i):
print(i)
i += 1
if i == 100:
return
recursive(i)
recursive(i)
# 출력
# 0
# 1
# 2
# ..
# ..
# 98
# 99재귀 함수 대표적인 예시
1. 팩토리얼 구현
def factorial(n):
if n <= 1:
return 1
return n * factorial(n-1)
print(factorial(5)) # 5! = 120
print(factorial(6)) # 6! = 720
2. 유클리드 호제법 (최대공약수 계산)
두 개의 자연수에 대한 최대공약수를 구하는 대표적인 알고리즘이다.
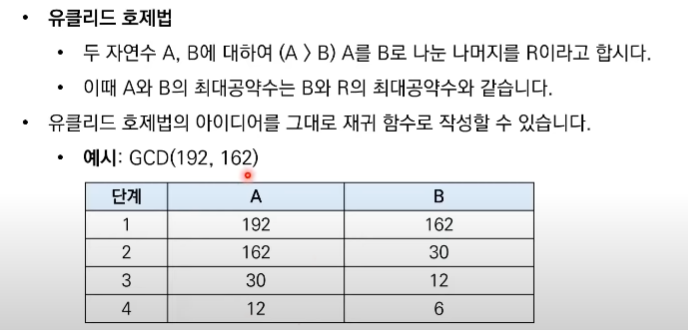
# a > b
def GCD(a, b):
if a % b == 0:
return b
else:
return GCD(b, a%b)
print(GCD(192, 162)) # print : 6
재귀 함수 사용 시 유의 사항

꼭 재귀 함수를 써야하는 건 아니다.
가독성이 떨어질 가능성도 있다.
DFS (Depth First Search)
깊이 우선 탐색, 깊은 부분을 우선적으로 탐색하는 알고리즘
DFS의 동작 과정

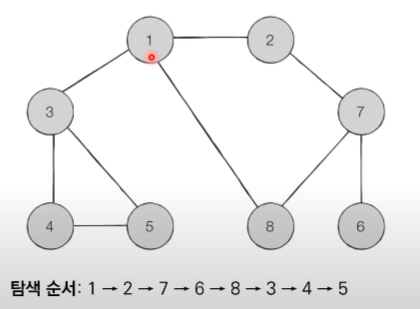
시작은 1이고, 인접한 노드들 중에 수가 낮은 것 부터 먼저 탐색한다고 가정했을 때
순서는 위와 같다.
파이썬 DFS 구현
def dfs(graph, v, visited):
# 시작 노드 방문 처리
visited[v] = True
# 방문 한 노드는 프린트
print(v, end=" ")
# 인접한 노드들을 돌면서, 방문하지 않은 노드를 방문
for i in graph[v]:
if not visited[i]:
dfs(graph, i, visited)
graph = [
[], # 없는 노드 처리
[2, 3, 8], # 1번 노드와 인접한 노드 번호
[1, 7], # 2번 노드와 인접한 노드 번호
[1, 4, 5], # 3번 노드와 인접한 노드 번호
[3, 5], # ..
[3, 4], #
[7], #
[2, 6, 8], #
[1, 7], # 8번 노드와 인접한 노드 번호
]
# 노드 번호와 순서 맞추기 위해 일부러 번호를 하나 크게 지정
visited = [False] * 9
# print : 1 2 7 6 8 3 4 5
dfs(graph, 1, visited)
BFS (Breadth-First Search)
너비 우선 탐색이라고 부르며, 그래프에서 가까운 노드부터 우선적으로 탐색하는 알고리즘
BFS는 큐 자료구조를 사용하며, 구체적인 동작 과정은 아래와 같다.
BFS의 동작 과정

인접한 노드들을 모두 방문하고 다음 노드로 넘어간다.
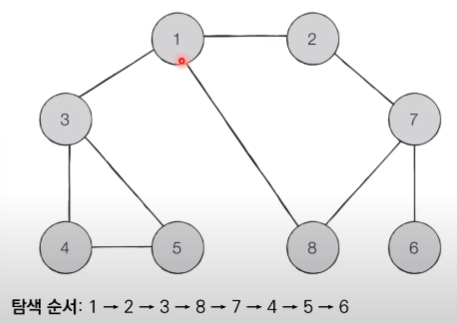
시작노드에서 인접한 노드들을 모두 큐에 넣고,
하나씩 방문하면서 방문한 곳의 인접한 노드들도 전부 넣는다.
파이썬 BFS 구현
from collections import deque
def bfs(graph, start, visited):
queue = deque([start])
# 시작 노드 방문 처리
visited[start] = True
# 큐가 빌 때까지 반복
while queue:
v = queue.popleft()
print(v, end=" ")
# 인접한 노드들을 돌면서, 방문하지 않은 노드를 방문
for i in graph[v]:
if not visited[i]:
queue.append(i)
visited[i] = True
graph = [
[], # 없는 노드 처리
[2, 3, 8], # 1번 노드와 인접한 노드 번호
[1, 7], # 2번 노드와 인접한 노드 번호
[1, 4, 5], # 3번 노드와 인접한 노드 번호
[3, 5], # ..
[3, 4], #
[7], #
[2, 6, 8], #
[1, 7], # 8번 노드와 인접한 노드 번호
]
# 노드 번호와 순서 맞추기 위해 일부러 번호를 하나 크게 지정
visited = [False] * 9
# print : 1 2 7 6 8 3 4 5
bfs(graph, 1, visited)'알고리즘 > 이론' 카테고리의 다른 글
| [자바스크립트] 그리디 (Greedy) 알고리즘 (0) | 2021.08.05 |
|---|---|
| [알고리즘] 이진 탐색 알고리즘 알기 (0) | 2021.01.14 |
| [알고리즘] 정렬 알고리즘 알기 (0) | 2021.01.13 |
| [알고리즘] 그리디 알고리즘 알기 (3) | 2021.01.08 |
| [이코테] 코딩 테스트 출제 경향 분석 및 파이썬 문법 부수기 (0) | 2021.01.06 |
![[알고리즘] DFS & BFS 알기](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FdPSrzV%2FbtqS1U157V7%2FAAAAAAAAAAAAAAAAAAAAAB-tP2cBNrGPIUmd360SAC75SjXJsNJ_99HxgkdbeQ9v%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3D8Q9i%252BlGpQ3BEuqlhWgQfFriJQdc%253D)